Linear Regression
Summarize the relationship between variables using a straight line drawn through the observed values of data

Complete the form below to unlock access to ALL audio articles.
Linear regression is a statistical method used to understand the relationship between an outcome variable and one or more explanatory variables. It works by fitting a regression line through the observed data to predict the values of the outcome variable from the values of predictor variables. This article will introduce the theory and applications of linear regression, types of regression and interpretation of linear regression using a worked example.
What is linear regression?
Scatter plots
Linear regression equation
Linear regression graph and the line of best fit
Types of linear regression analysis
Simple linear regression
- Simple linear regression formula
- Simple linear regression model – worked example
What is multiple linear regression?
- Multiple linear regression formula
- Multiple linear regression model – worked example continued
Non-linear regression
Assumptions of linear regression
Ordinary vs Bayesian linear regression
Linear regression vs logistic regression
Linear regression in machine learning
Linear regression example
What is linear regression?
Linear regression is a powerful and long-established statistical tool that is commonly used across applied sciences, economics and many other fields. Linear regression considers the relationship between an outcome (dependent or response) variable and one or more explanatory (independent or predictor) variables, where the variables under consideration are quantitative (or continuous, e.g. age, height). In other words, linear regression enables you to estimate how (by how much and in which direction, positive or negative) the outcome variable changes as the explanatory variable changes.
It summarizes the relationship between the variables using a straight line drawn through the observed values of data. A first step in understanding the relationship between an outcome and explanatory variable is to visualize the data using a scatter plot, through which the regression line can be drawn.
Scatter plots
Scatter plots are diagrams that can help investigate the relationship between an outcome and predictor variable, by plotting the outcome variable on the vertical y-axis, an explanatory variable on the horizontal x-axis and markers representing the observed values of each variable in the dataset. Not only can they help us visually inspect the data, but they are also important for fitting a regression line through the values as will be demonstrated. See Figure 1 for an example of a scatter plot and regression line.
A closely related method is Pearson’s correlation coefficient, which also uses a regression line through the data points on a scatter plot to summarize the strength of an association between two quantitative variables. Linear regression takes the logic of the correlation coefficient and extends it to a predictive model of that relationship. Some key advantages of linear regression are that it can be used to predict values of the outcome variable and incorporate more than one explanatory variable.
Linear regression equation
The linear regression equation is perhaps one of the most recognizable in statistics. It can be used to represent any straight line drawn on a plot:
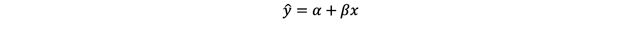
Where ŷ (read as “y-hat”) is the expected values of the outcome variable and x refers to the values of the explanatory variable.
The equation helps us relate these y and x values. The value α is the intercept, the point at which the regression line cuts the y-axis (in other words, the point at which the explanatory variable is equal to 0). Often, the intercept may not have any relevant interpretation. The value β is the slope of the regression line, also referred to as the regression coefficient, which is the expected change (either increase or decrease) in y every time x increases by 1 unit.
Linear regression graph and the line of best fit
To fit the straight line through the data, the method minimizes the vertical distance between the line and each point so that the line fit is that which is closest to all the data points. The distance between the line and the observed values is known as a residual, ε. For each observed value of y, the regression equation then becomes:
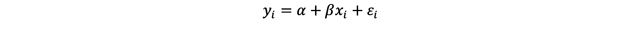
Where εi is the residual difference between the value of y predicted by the model (ŷ) and the measured value of y. The resulting regression line is displayed in Figure 1.

Figure 1: Scatter plot showing an outcome variable (blood pressure) on the y-axis and explanatory variable (age) on the x-axis, with regression line through the plots. Credit: Technology Networks.
Types of linear regression analysis
Simple linear regression examines the relationship between one outcome variable and one explanatory variable only. However, linear regression can be readily extended to include two or more explanatory variables in what’s known as multiple linear regression.
Simple linear regression
- Simple linear regression formula
As detailed above, the formula for simple linear regression is:
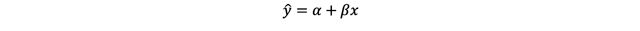
or
![]()
for each data point
- Simple linear regression model – worked example
Let’s say we are interested in examining the relationship between blood pressure (BP) and age (in years) in a hospital ward.
We can start by plotting our outcome variable (BP) on the y-axis and explanatory variable (age) on the x-axis, as shown in Figure 1. The general form of a simple linear regression line is as follows:
![]()
When we analyze the data, we find that the intercept (α) = 121.1 and the slope (β) = 0.4. The regression line is then:
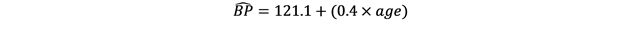
We can interpret β as meaning that for each unit (year) increase in age the BP increases by 0.4, on average. The intercept α is the point at which the line cuts the y-axis, so we can interpret it as the BP value at birth (where age is equal to 0).
A useful capability of linear regression is predicting a value of the outcome variable given a value of the explanatory variable using the regression line. This predicted mean is calculated by substitution of the explanatory value in the regression equation. For example, if we were interested in that of a 25-year-old in our sample:
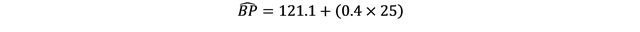
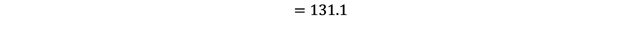
In general, it is not advised to predict values outside of the range of the data collected in our dataset.
What is multiple linear regression?
Often in applied settings, researchers are interested in the interplay between many possible explanatory factors to predict values of an outcome variable (for example, in a single dataset we may have information on age, sex, ethnicity and weight) and may want to adjust for them to improve identification of the effects of a main variable of interest. Involving multiple explanatory variables adds complexity to the method, but the overall principles remain the same.
- Multiple linear regression formula
The equation for multiple linear regression extended to two explanatory variables (x1 and x2) is as follows:

This can be extended to more than two explanatory variables. However, in practice it is best to keep regression models as simple as possible as it is less likely to violate the assumptions.
- Multiple linear regression model – worked example continued
Let’s say in our study we also collected patients’ weight in kilograms (kg). We may know from previous studies that weight can interfere with the effect of age on BP (known as a confounding factor) and therefore we want to adjust for it. The regression equation would now look like this:
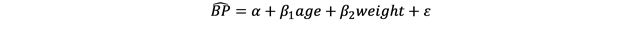
And let’s say we calculate both regression coefficients for this model and find the following:
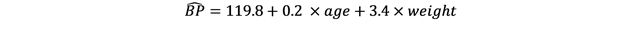
We can interpret α as both age and weight crossing the y-axis at a BP value of 119.8. For the coefficients, for each year increase in age, the BP increases by 0.2 while adjusting for weight. Similarly, for each kg increase in weight the BP increases by 3.4 while adjusting for age. You will notice that the coefficient for age has decreased by about half (0.4 vs 0.2) when adjusting for the effect of weight, compared with the simple linear regression including only age. This tells us that there is an interplay between the two explanatory variables and highlights the importance of variable adjustment in multiple linear regression.
Non-linear regression
We have discussed the basis of linear regression as fitting a straight line through a plot of data. However, there may be circumstances where the relationship between the variables is non-linear (i.e., does not take the shape of a straight line), and we can draw other shaped lines through the scatter of plots (Figure 2). A method commonly used to fit non-linear curves to data instead of straight regression lines is polynomial regression. This method uses the same principles as linear regression but models the relationship between explanatory and outcome variables differently, where increasing degrees of polynomial fits to more complex curving patterns in the data.
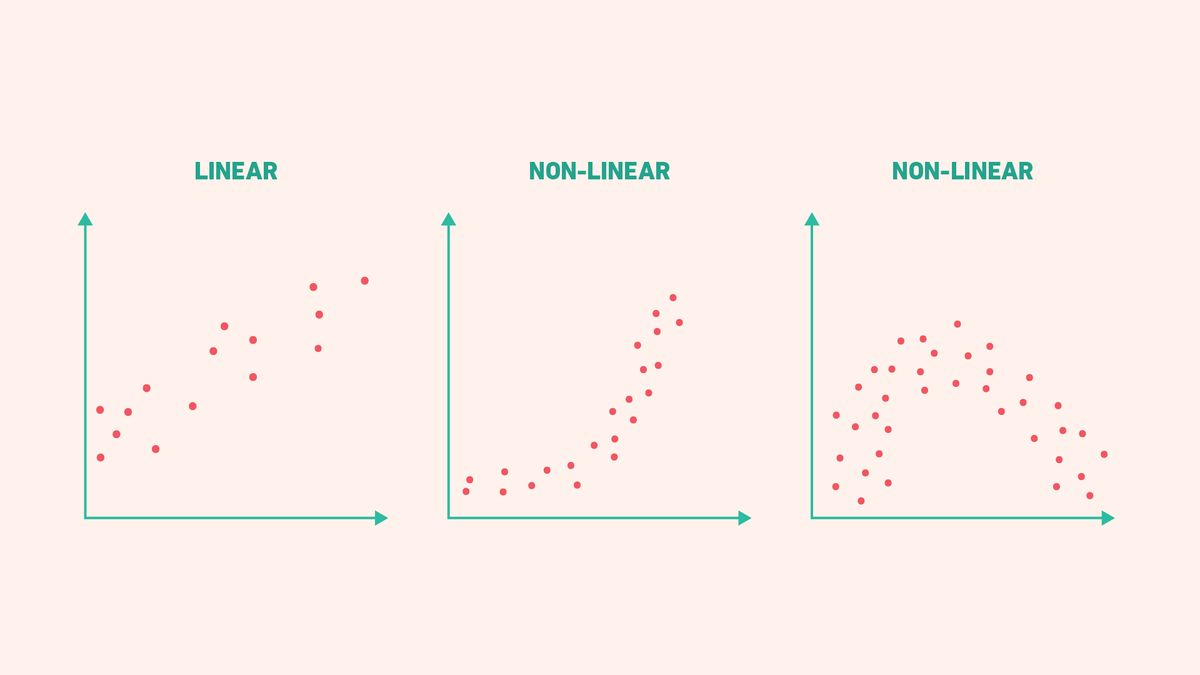
Figure 2: Examples of scatter plots where the relationship between the outcome and explanatory variables takes both linear and non-linear shapes. Credit: Technology Networks.
Assumptions of linear regression
Linear regression producing interpretable and valid estimates relies on making certain assumptions about the data, as follows:
- Normality: that the data follows a Normal distribution.
- Independence: that the observations in the dataset are unrelated to one another and were collected as part of a random sample of a population.
- Homoscedasticity: also known as homogeneity of variance, that the size of the error in the regression prediction does not vary greatly across values of the explanatory variable.
- Linearity: that the relationship between the explanatory and outcome variable is linear, and that the line of best fit through the data is a straight line.
An additional assumption for multiple linear regression is that of no collinearity between the explanatory variables, meaning they should not be highly correlated with each other to allow reliable predictions of the outcome values.
Ordinary vs Bayesian linear regression
Linear regression can be done under the two schools of statistics (frequentist and Bayesian) with some important differences. Briefly, frequentist statistics relies on repeated sampling and probability theory and is the type of regression we have focused on in this article. Bayesian statistics considers prior information with the observed data to make inferences and learn from data.
Linear regression vs logistic regression
Logistic regression is another commonly used type of regression. This is where the outcome (dependent) variable takes a binary form (where the values can be either 1 or 0). Many outcome variables take a binary form, for example death (yes/no), therefore logistic regression is a powerful statistical method. Table 1 outlines the key differences between these two techniques.
Table 1: Summary of some key differences between linear and logistic regression.
| Element | Linear regression | Logistic regression |
| Outcome variable | Models continuous outcome variables | Models binary outcome variables |
| Regression line | Fits a straight line of best fit | Fits a non-linear S-curve using the sigmoid function |
| Linearity assumption | Linear relationship between the outcome and explanatory variables needed | Linear relationship not needed/relevant |
| Estimation | Usually estimated using the method of least squares | Usually estimated using maximum likelihood estimation (MLE) |
| Coefficients | Model coefficients represent change in outcome variable for every unit increase in an explanatory variable | Model coefficients represent change in log odds of the outcome for every unit increase in an explanatory variable |
Linear regression in machine learning
In the field of machine learning, linear regression can be considered a type of supervised machine learning. In this use of the method, the model learns from labeled data (a training dataset), fits the most suitable linear regression (the best fit line) and predicts new datasets. The general principle and theory of the statistical method is the same when used in machine learning or in the traditional statistical setting. Due to the simple and interpretable nature of the model, linear regression has become a fundamental machine learning algorithm and can be particularly useful for complex large datasets and when incorporating other machine learning techniques.
Linear regression example
It is common practice to conduct a hypothesis test for the association between an explanatory variable and outcome variable based on a linear regression model. This allows us to draw conclusions from the model while taking account of the uncertainty inherent in this kind of analysis, acknowledging that the coefficients are estimates.
In the worked example we already considered above, if we run the multiple linear regression, we would generate a 95% confidence interval (CI) around the regression coefficient for age, which is a quantitative measure of uncertainty around the estimate that may look something like 0.2 (95% CI 0.12–0.25). This can be interpreted as the true change in BP for each year increase in age is between 0.12 and 0.25. Given this is a relatively small range, this indicates low uncertainty in our estimate of β.
The 95%CI is derived using a t-distribution, which is a probability distribution commonly used in statistics. The t-distribution can also be used to conduct a hypothesis test of the linear regression, where the hypotheses are as follows:
- Null hypothesis H0: that there is no change in BP with each unit change in age (β = 0).
- Alternative hypothesis H1: there is a linear change in BP with each unit change in age β ≠0)
We would calculate a t statistic (usually done using statistical software) and use this to calculate a p-value (a probability of obtaining statistical test results as extreme as the observed results). In our example, we find a p-value of p < 0.001, indicating strong evidence against the null hypothesis of no association between change in BP and age, also reflected in the 95% CI.
Further reading
- Bland M. An Introduction to Medical Statistics (4th ed.). Oxford. Oxford University Press; 2015. ISBN:9780199589920
- Geeksforgeeks. Linear regression in machine learning. Geeksforgeeks. https://www.geeksforgeeks.org/ml-linear-regression/. Published 2025. Accessed Jan 29, 2025.
- Newcastle University. Simple linear regression. Newcastle University. https://www.ncl.ac.uk/webtemplate/ask-assets/external/maths-resources/statistics/regression-and-correlation/simple-linear-regression.html. Accessed Jan 29, 2025.
- Bevans R. Multiple linear regression: A quick guide (examples). Scribbr. https://www.scribbr.com/statistics/multiple-linear-regression/. Published 2020. Accessed Jan 29, 2025.